阻挫磁体中的量子自旋液体是凝聚态物理理论研究的难点与突破点，这种由于量子涨落和磁阻挫的结合而在强关联的电子系统中涌现出的奇异物质形态，自上世纪70年代诺贝尔奖得主 P.W. Anderson 提出以来，反复出现在凝聚态物理研究的各个方向。它可能是最终理解高温超导机制的钥匙，可能是拓扑量子计算的载体，而且更有可能意味着现有的以对称性自发破缺为基础的凝聚态相变理论需要做重大的改写甚至重写，因此，对于量子自旋液体的研究，具有重大理论和实际意义。但是由于这些系统及其复杂，展现出量子涨落、磁阻挫、基态拓扑简并、拓扑量子序和长程量子纠缠等等效应，解析的方法已经难以提供定量的结果。面对如此困难，以量子蒙特卡洛模拟为代表的无偏差或少偏差的数值方法，随着计算机性能的突飞猛进，在这些艰深的课题上体现出了力量，帮助人们扩展对于阻挫磁体和其中存在的量子自旋液体、量子自旋冰和团簇莫特绝缘体的认识。
　　量子自旋冰是三维的量子自旋液体，而团簇莫特绝缘体则是更广义的概念，一般把1/2晶格占据的玻色子团簇莫特绝缘体称作量子自旋冰。量子自旋冰是从经典自旋冰发展而来的概念，经典自旋冰主要存在于 pyrochlore lattice 材料之中，比如Dy2Ti2O7 “Nature 399, 333 (1999)”，Ho2Ti2O7 “Science 326, 415 (2009)”。这些材料中的稀有金属元素存在于 corner sharing 的四面体顶点上。由于四面体的顶点之间的磁性相互作用存在几何阻挫，故而系统在极低温度是仍有熵存留，并且自旋构型满足“两进两出”的 Pauling ice rule。经典自旋冰中由于几何阻挫的存在，系统中的磁激发可以用磁单级子的形式来描述 “Nature 451, 42 (2008)”。在经典自旋冰中加入量子自旋涨落，从理论上讲就可能出现量子自旋冰，或者团簇莫特绝缘体。在量子自旋冰和团簇莫特绝缘体中除了有分数化的磁单级子的激发之外，还涌现出满足量子电动力学层展U(1)规范场理论所描述的低能“光子”。这样的物质形态不能用传统的以对称性自发破缺为基础的凝聚态相变理论来描述，它们的存在对凝聚态理论提出了新的问题，而且将量子电动力学层展规范场理论和凝聚态理论，以及阻挫磁体的材料制备和物性测量，进行了有益的结合。量子蒙特卡洛模拟可以为量子自旋冰和团簇莫特绝缘体系统的研究提供定量的数值结果。
　　最近，中国科学院物理研究所/北京凝聚态物理国家实验室（筹）理论室T03组孟子杨副研究员，与安徽师范大学吕建平副教授，复旦大学陈钢教授还有中国科技大学邓友教授组成的研究团队，运用量子蒙特卡洛蠕虫算法，使用天津国家超算中心“天河1号”超级计算机和其他计算平台，研究了三维阻挫磁体中可能存在的量子自旋冰和团簇莫特绝缘体。
　　他们运用大规模量子蒙特卡洛并行计算，世界上第一次完整地给出了硬壳玻色子在pyrochlore lattice 上，以玻色子占据数和相互作用强度的为轴的二维相空间中的相图，发现了1/4 和3/4 玻色子占据的两种团簇莫特绝缘体，证实了1/4, 1/2和3/4 玻色子占据的团簇莫特绝缘体（其中1/2 玻色子占据的团簇莫特绝缘体就是量子自旋冰）是具有量子电动力学层展U(1) 规范场特性的奇异物质形态；而且，通过比热和电场关联函数的综合测量直接观测到团簇莫特绝缘体中的层展U(1)规范场。他们预计很多阻挫磁体材料都可能是团簇莫特绝缘体,而且为接下来与物理所和国内现有的材料合成、中子散射、RIXS 散射等实验团队进行合作，填补国内在阻挫磁体（量子自旋液体、量子自旋冰、团簇莫特绝缘体）这些方面的空白，尽快在世界发展前沿中占有一席之地奠定了基础。
　　这项研究成果最近发表在Phys. Rev. Lett. 115, 037202 (2015)。该工作得到了国家青年千人计划（孟子杨），中科院物理所国际合作交流中心（陈钢）， 国家自然科学基金（吕建平，邓友金）和中国科学院的支持。 由于量子蒙特卡洛模拟需要进行大规模的并行计算，这项工作也到了天津国家超算中心的有力配合。
 

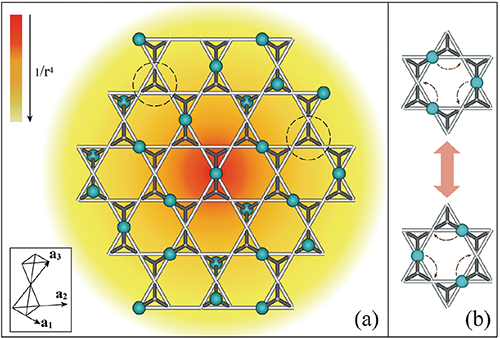
Fig. 1. (a) （示意图）1/4 玻色子占据的团簇莫特绝缘体。晶格是三维pyrochlore lattice 的二维 kagome 平面投影，每个四面体中有一个玻色子占据。当在系统中加入或者拿出一个玻色子后，会造成两个分数化的激发，如图中虚线圆圈所示。背景的颜色代表了团簇莫特绝缘体中的1/r^4 的电场关联函数，这是量子电动力学层展U(1)规范场理论的预言，被我们的量子蒙特卡洛计算所证实。(b) （示意图）团簇莫特绝缘体中的无能隙激发，由三个玻色子在kagome 平面上的六边形中的集体运动构成， 这种激发是量子电动力学层展U(1)规范场理论预言中的”光子“，被我们的量子蒙特卡洛计算所证实。 制图：理论室T03组博士研究生许霄琰。

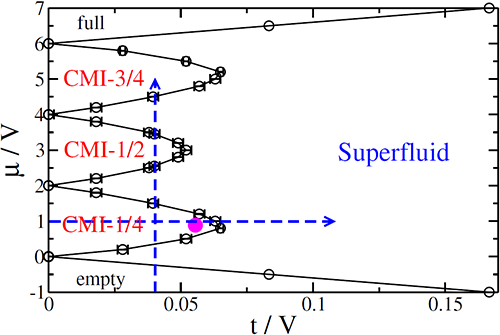Fig. 2. 量子蒙特卡洛计算中得到的硬壳玻色子在 pyrochlor lattice 中的相图。横轴是玻色子之间相互作用的强度，纵轴是系统的化学势（控制玻色子占据数）。当玻色子的动能主导时，系统处于超流体的状态 (Superfluid)，当玻色子之间的相互作用主导时，在晶格的阻挫和量子涨落的结合作用下，系统涌现出三个团簇莫特绝缘体态，分别对应于玻色子1/4 占据(CMI-1/4)，1/2 占据(CMI-1/2)和 3/4占据(CMI-3/4)。CMI 代表 cluster Mott insulator，一般把1/2 玻色子占据的的团簇莫特绝缘体称为量子自旋冰。

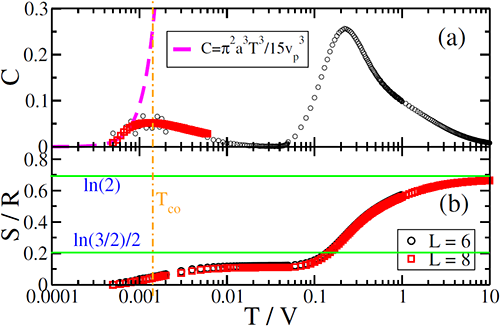Fig. 3. 1/4玻色子占据的团簇莫特绝缘体中比热和熵随温度的关系。(a). 随着温度的降低，比热经过两个转变，分别发生在 T~V 和 T~V/1000， 对应于从顺磁态到经典自旋冰的转变和从经典自旋冰到团簇莫特绝缘体的转变。在团簇莫特绝缘体中，从比热和温度的依赖关系中可以估计出光子的光速，这是层展U(1)规范场存在的直接证据。(b). 与之相对应的，在高温时，系统展现顺磁态的熵 ln(2)；进入经典自旋冰的中间温度范围，由于磁阻挫造成简并，系统的熵处在一个平台，不随温度的降低而变化；更低温时，系统进入1/4 玻色子占据的团簇莫特绝缘体，量子涨落解除了系统的简并，熵减小到零。

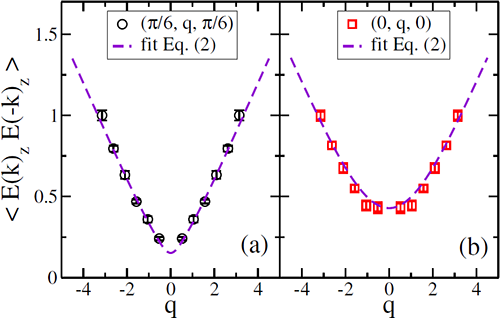
Fig. 4. 1/4玻色子占据的团簇莫特绝缘体中涌现的电场关联函数。电场来源于 Fig. 1 (b) 中的玻色子集体低能激发，是量子电动力学层展U(1)规范场对于团簇莫特绝缘体的预言，它的存在被我们的计算所证实，这是层展U(1) 规范场的直接证据。 (a), (b) 是电场在不同动量方向的关联，从这些数据可以估计出层展U(1)规范场中光子的光速，这里所得到的光速与比热测量中估计出的光速是一致的。 转载自：http://www.iop.cas.cn/xwzx/kydt/201507/t20150717_4394874.html